Quadrupole strengths to be varied

The problem here is to relate quadrupole names to the strength names.  We have a provisional function for that.

"index_289.gif"

MQ.12R2.B1:MQ,             AT= 490.0647+(143-IP2OFS.B1)*DS,       from= IP2;;
MQ.12R2.B1,                K1 := kqf.a23;;
MQ.12R2.B1, APERTYPE=RECTELLIPSE, APERTURE={0.022, 0.01715, 0.022, 0.022};;

"index_290.gif"

"index_291.gif"

"index_292.gif"

"index_293.gif"

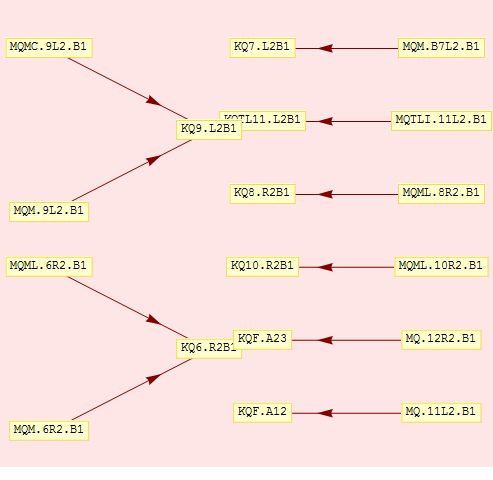
This allows us to create strength hierarchy trees and see which elements are on common power converters.

"index_294.gif"

"index_295.gif"

"index_296.gif"

"index_297.gif"

"index_299.gif"

"index_300.gif"

"index_301.gif"

"index_302.gif"

MQT.13L2.B1 KQT13.L2B1 1.387 -0.00119592 0.00526778
MQ.13L2.B1 KQF.A12 4.785 0.0089901 0.00955053
MQT.12L2.B1 KQT12.L2B1 54.8385 0.00315173 0.00526778
MQ.12L2.B1 KQD.A12 58.2365 -0.00860096 0.00955053
MQ.11L2.B1 KQF.A12 111.47296819305907.047169565250538 0.0089901 0.00955053
MQTLI.11L2.B1 KQTL11.L2B1 112.94196819305905.05285535173747 0.000150509 0.00535343
MQML.10L2.B1 KQ10.L2B1 164.76165759074561.216856152542043 -0.00624671 0.00856549
MQMC.9L2.B1 KQ9.L2B1 201.45964698843213.304188068614593 0.00648015 0.00856549
MQM.9L2.B1 KQ9.L2B1 205.22564698843217.312231633484352 0.00648015 0.00856549
MQML.8L2.B1 KQ8.L2B1 244.29363638611869.387912154167914 -0.00418719 0.00856549
MQM.B7L2.B1 KQ7.L2B1 281.96162578380529.45019000603437 0.00680255 0.00856549
MQM.A7L2.B1 KQ7.L2B1 285.72862578380528.455953752448455 0.00680255 0.00856549
MQML.6L2.B1 KQ6.L2B1 305.40862578380541.484881298854674 -0.00459638 0.0068524
MQM.6L2.B1 KQ6.L2B1 309.17562578380540.49020524849064 -0.00459638 0.0068524
MQY.B5L2.B1 KQ5.L2B1 377.34662578380568.576740470903474 0.00479196 0.0068524
MQY.A5L2.B1 KQ5.L2B1 381.12762578380597.581070429461306 0.00479196 0.0068524
MQY.B4L2.B1 KQ4.L2B1 407.08562578380639.60968576768771 -0.00548167 0.0068524
MQY.A4L2.B1 KQ4.L2B1 410.86662578380668.613700865460974 -0.00548167 0.0068524
MQXA.3L2 KQX.L2 499.79162578380726.69878897506704 0.0094221 0.00877963
MQSX.3L2 KQSX3.L2 500.26012578380727.69919588796797 0. 0.0034262
MQXB.B2L2 KQX.L2-KTQX2.L2 508.20662578380728.706040322899685 -0.0094221 0.00877963
MQXB.A2L2 KQX.L2-KTQX2.L2 514.70662578380734.711559758929837 -0.0094221 0.00877963
MQXA.1L2 KQX.L2+KTQX1.L2 523.79162578380726.719158550780783 0.0094221 0.00877963
MQXA.1R2 KQX.R2+KTQX1.R2 576.09162578380801.760491562256007 -0.0094221 0.00877963
MQXB.A2R2 KQX.R2-KTQX2.R2 584.30662578380793.766640811049324 0.0094221 0.00877963
MQXB.B2R2 KQX.R2-KTQX2.R2 590.80662578380793.77144535719714 0.0094221 0.00877963
MQSX.3R2 KQSX3.R2 593.47612578380790.773403252947055 0. 0.0034262
MQXA.3R2 KQX.R2 600.09162578380790.77821756627408 -0.0094221 0.00877963
MQY.A4R2.B1 KQ4.R2B1 686.04662578380885.836353632663755 0.0049106 0.0068524
MQY.B4R2.B1 KQ4.R2B1 689.82762578380914.83874058273248 0.0049106 0.0068524
MQM.A5R2.B1 KQ5.R2B1 715.78562578381013.8547829727555 -0.0048499 0.0068524
MQM.B5R2.B1 KQ5.R2B1 719.56662578381042.857071012130362 -0.0048499 0.0068524
MQML.6R2.B1 KQ6.R2B1 789.13762578381045.897152750872554 0.00431202 0.0068524
MQM.6R2.B1 KQ6.R2B1 792.90462578381050.899220951520842 0.00431202 0.0068524
MQM.A7R2.B1 KQ7.R2B1 810.67162578381067.90884497259644 -0.00610131 0.00856549
MQM.B7R2.B1 KQ7.R2B1 814.43862578381061.91085836244722 -0.00610131 0.00856549
MQML.8R2.B1 KQ8.R2B1 853.50863638612475.931207919962603 0.00562514 0.00856549
MQMC.9R2.B1 KQ9.R2B1 890.20464698843887.949489857028247 -0.00551556 0.00856549
MQM.9R2.B1 KQ9.R2B1 893.97064698843894.951323259220715 -0.00551556 0.00856549
MQML.10R2.B1 KQ10.R2B1 933.03665759075318.96989870685115 0.00732671 0.00856549
MQ.11R2.B1 KQD.A23 983.42736819306731.99274229027694 -0.00860096 0.00955053
MQTLI.11R2.B1 KQTL11.R2B1 984.89636819306725.993390535990358 -0.00106338 0.00535343
MQT.12R2.B1 KQT12.R2B1 1034.96788409653850.014926873487568 -0.0029105 0.00526778
MQ.12R2.B1 KQF.A23 1038.36588409653840.0163504107814 0.0089901 0.00955053
MQT.13R2.B1 KQT13.R2B1 1088.41640000000940.036795077003205 -0.00266927 0.00526778
MQ.13R2.B1 KQD.A23 1091.81440000000930.038148817941458 -0.00860096 0.00955053

"index_304.gif"

"index_307.gif"

"index_310.gif"

"index_311.gif"

"index_312.gif"

We need to group duplicate strengths and take the one with the smallest K1MAX.

"index_313.gif"

"index_314.gif"

"index_315.gif"

"index_316.gif"

"index_319.gif"

"index_320.gif"

VARY, NAME=KQ10.L2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ10.R2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ4.R2B1, STEP=1.E-9, LOWER=-0.006852395389181927, UPPER=0.006852395389181927;
VARY, NAME=KQ5.L2B1, STEP=1.E-9, LOWER=-0.006852395389181927, UPPER=0.006852395389181927;
VARY, NAME=KQ5.R2B1, STEP=1.E-9, LOWER=-0.006852395389181927, UPPER=0.006852395389181927;
VARY, NAME=KQ6.L2B1, STEP=1.E-9, LOWER=-0.006852395389181927, UPPER=0.006852395389181927;
VARY, NAME=KQ6.R2B1, STEP=1.E-9, LOWER=-0.006852395389181927, UPPER=0.006852395389181927;
VARY, NAME=KQ7.L2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ7.R2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ8.L2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ8.R2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ9.L2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQ9.R2B1, STEP=1.E-9, LOWER=-0.008565494236477409, UPPER=0.008565494236477409;
VARY, NAME=KQD.A23, STEP=1.E-9, LOWER=-0.00955052607367231, UPPER=0.00955052607367231;
VARY, NAME=KQT12.R2B1, STEP=1.E-9, LOWER=-0.005267778955433606, UPPER=0.005267778955433606;
VARY, NAME=KQTL11.L2B1, STEP=1.E-9, LOWER=-0.00535343389779838, UPPER=0.00535343389779838;
VARY, NAME=KQTL11.R2B1, STEP=1.E-9, LOWER=-0.00535343389779838, UPPER=0.00535343389779838;

Now repeat all that, modified for Beam2

"index_322.gif"

"index_324.gif"

"index_327.gif"

"index_330.gif"

"index_333.gif"

Created by Wolfram Mathematica 6.0  (30 August 2007) Valid XHTML 1.1!